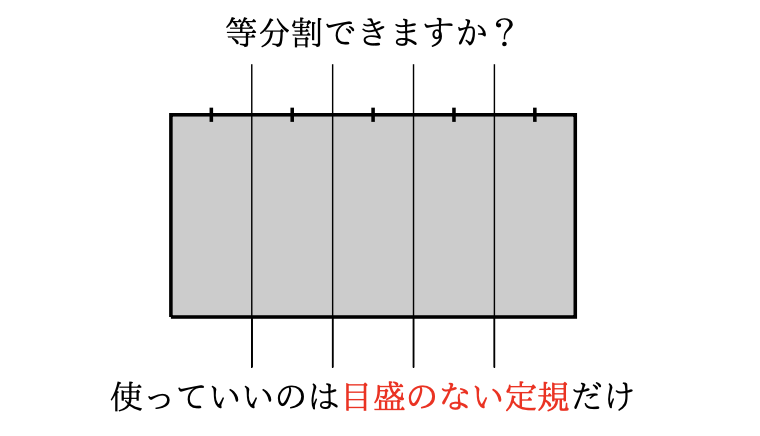
長方形のケーキを,ナイフだけを用いて複数人に公平に切り分けたくなったことはないでしょうか.そしてそれは数学的に可能なのでしょうか.問題を次のように言い換え,考えてみましょう.
$n$ を $2$ 以上の自然数とする.任意に与えられた長方形に対して,その辺の $n$ 等分点を目盛のない定規のみを用いて作図することは出来るか.
ただし目盛のない定規でできることは「与えられた $2$ 点を結ぶ直線を引くこと」だけで,長さを測ることはできないものとします.一般的な作図問題ではコンパスも使うことができますが,今回はそれが使えない状況を考えているということです.
結論から言うと,問の答えは(任意の $n$ に対して)Yesとなります.このことを示しましょう.そのためには,次の命題を言えば十分です.
線分 $AB$ および $AB$ と平行であってそれを含まない直線 $l$ が与えられたとする.このとき,$AB$ の $n$ 等分点は作図可能.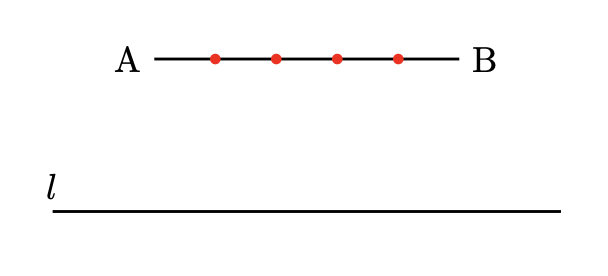
証明
まず $n=2$ の場合について示す.直線 $AB$ および $l$ 上にない点$C$を任意に取る.$AC$ と $l$ の交点を $D$, $BC$ と $l$ の交点を $E$ とする.さらに,$AE$ と $BD$ の交点を $F$ とし,$CF$ と $AB$ の交点を $G$ とする.
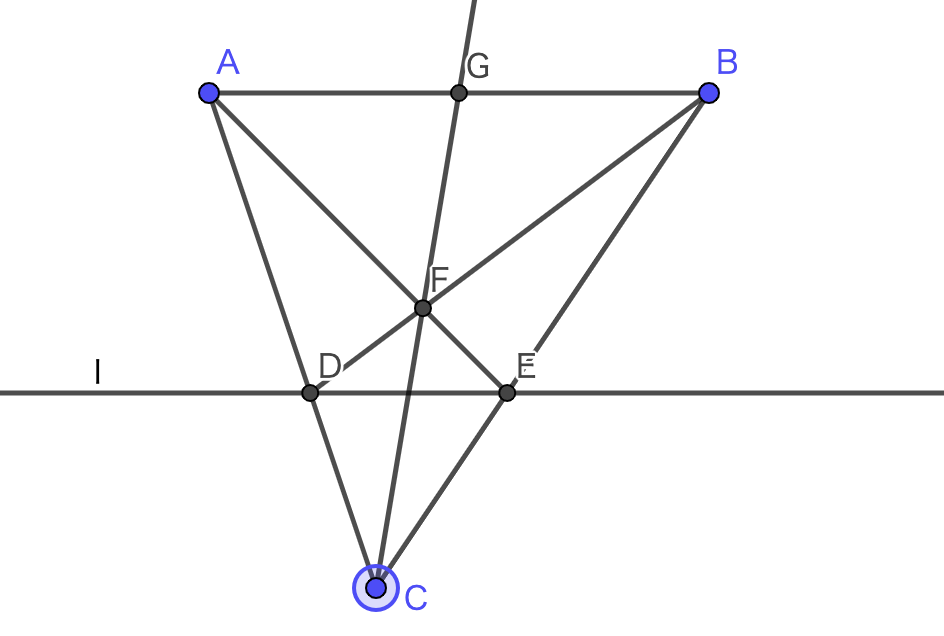 $n=2$ の場合
$n=2$ の場合このとき $G$ は $AB$ の中点である.実際,チェバの定理から\[\frac{DC}{AD} \cdot \frac{EB}{CE} \cdot \frac{GA}{BG}=1\]であるが,$AB$ と $l$ が平行であることから\[\frac{DC}{AD} \cdot \frac{EB}{CE}=1\]である.したがって\[\frac{GA}{BG}=1\]となり,$G$ は $AB$ の中点であることが分かる.
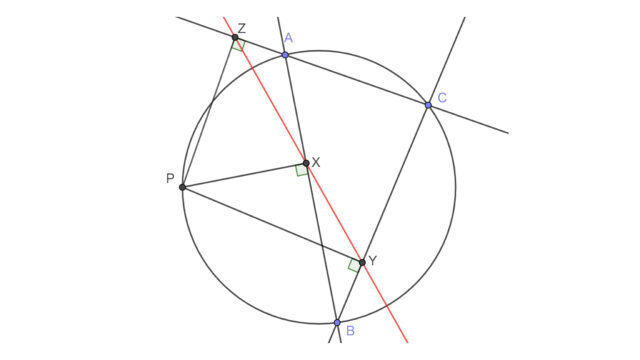
次に$n \geq 3$ の場合を考える.もし $n=2^k\ (k\ \text{は整数})$ の形で書けるなら,$n=2$ の場合の方法を繰り返し適用して $AB$ を $n$ 等分すればよい.以下,そうでない場合を考える.$m$ を$m>\log_2{n}$を満たす最小の整数とする.$n=2$ の場合の方法を繰り返すことで $DE$ の $2^m$ 等分点が作図できる.それらを $D$ に近い方から順に $P_1,P_2,\dots,P_{2^m-1}$ とし,$BP_n$ と $AC$ の交点を $P$ とする.さらに$i=1,2,\dots,n-1$に対し, $PP_i$ と $AB$ の交点を$Q_i$ とする.このとき,$Q_1,\dots,Q_{n-1}$ は $AB$ の $n$ 等分点である.
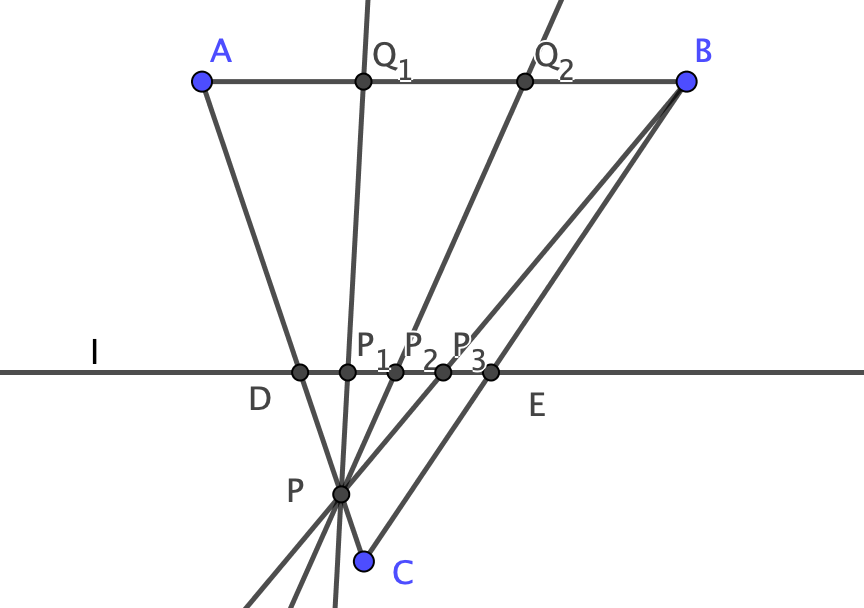 $n=3$ の場合
$n=3$ の場合以上を合わせて命題を示せた.
3等分や5等分はもちろん,何等分であっても理論的上可能ということですね!