ピザの定理（Pizza theorem）と呼ばれる，円板の面積を等分割する方法に関する定理が知られています．本記事ではピザの定理の主張とその証明を紹介します．
ピザの定理
ピザの定理の主張は，次のとおりです．
半径 $1$ の円 $C$ と，その内側に含まれる点 $P$ を考える．$l_1$ を $P$ を通る直線とし，$h_1$ を $P$ を通り $l_1$ と垂直な直線とする．さらに $\theta$ を $0 \leq \theta \leq \pi/2$ を満たす実数とし，$l_1,\ h_1$ を $P$ を中心に $\theta$ （rad）反時計回りに回転させて移る直線をそれぞれ $l_2,\ h_2$ とする．
このとき $l_1,l_2,C$ で囲まれる領域の面積と $h_1,h_2,C$ で囲まれる領域の面積の和を $S(\theta)$とすると， $S(\theta)=2\theta$ が成り立つ．
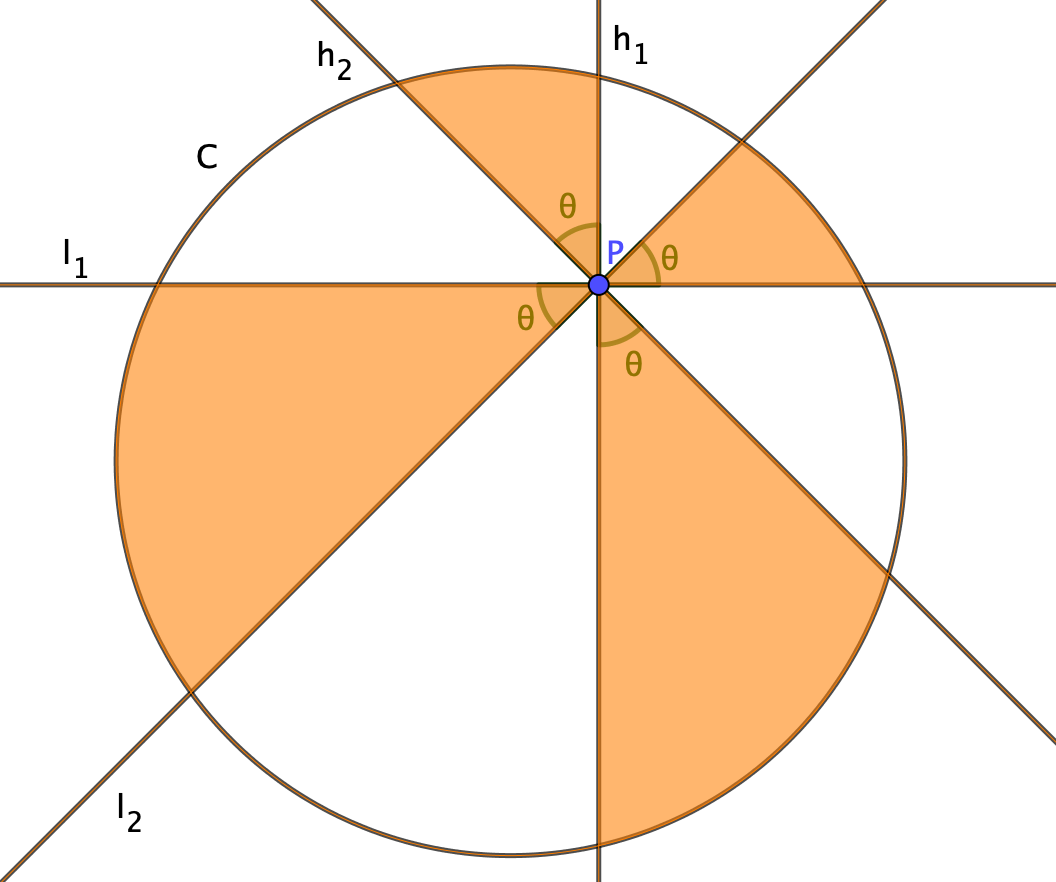$S(\theta)$（橙色の領域の面積）は $2\theta$ である．ピザの定理の証明
証明には次の補題を用います．
円 $C$, 点 $P$ および 直線 $l_1,\ h_1$ を定理1のように定める．また，以下の図のように $C$ と $l_1$ の共有点を $X,\ Y$，$C$ と $h_1$ の共有点を $Z,\ W$ と名づける．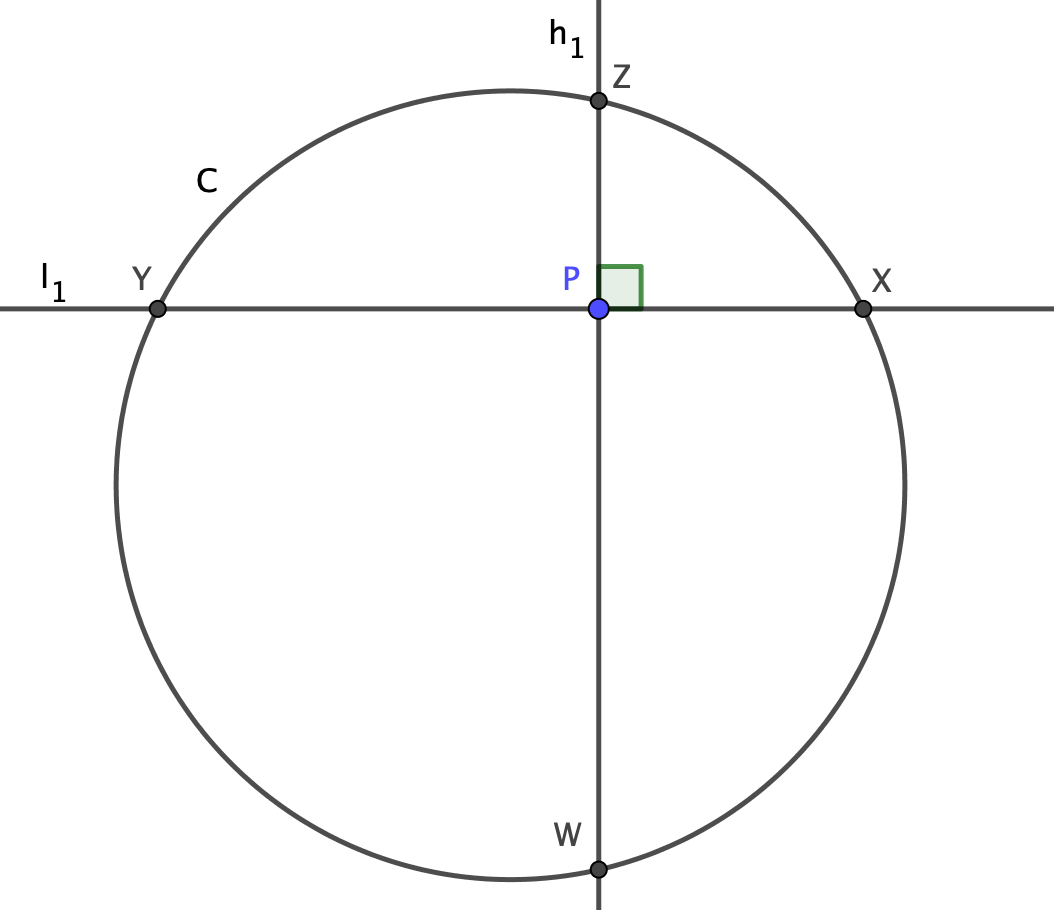
このとき，$$PX^2+PY^2+PZ^2+PW^2=4$$が成り立つ．
一旦この補題を認めて，定理１を証明しましょう．
定理１の証明．
円 $C$ の内側の点 $P$ および $P$ を通る直線 $l_1$ を任意にとり，固定する．以下の図のように $C$ と $l_2$ の共有点を $X(\theta),\ Y(\theta)$，$C$ と $h_2$ の共有点を $Z(\theta),\ W(\theta)$ と名づける．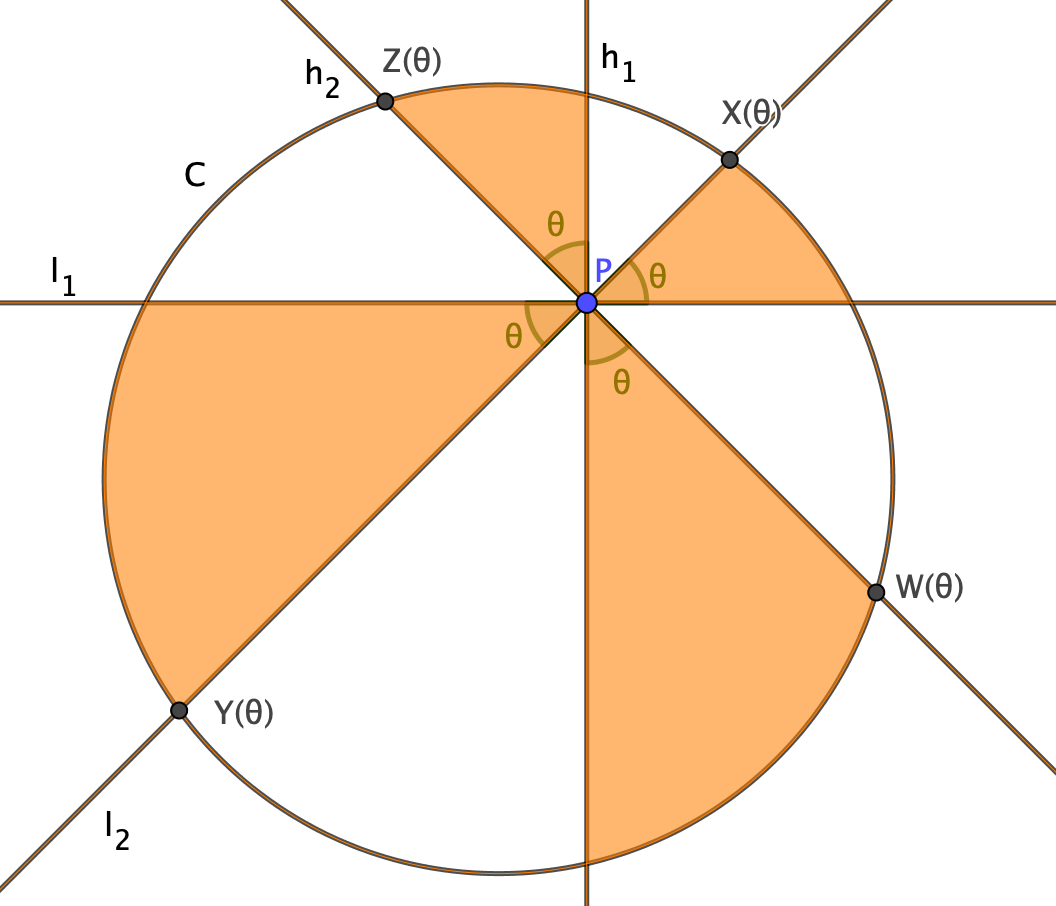
いま，極方程式の面積公式から$$\begin{aligned}S(\theta)=&\frac{1}{2}\int_0^\theta \{PX(\theta)^2+PY(\theta)^2\\&\quad+PZ(\theta)^2+PW(\theta)^2\}d\theta\end{aligned}$$が成り立つ．ここで補題２より右辺の被積分関数の値は $\theta$ に依存せず $4$ なので，$$\begin{aligned}S(\theta)&=\frac{1}{2}\int_0^\theta 4\ d\theta \\&=2\theta\end{aligned}$$となって，定理１が示せる．
補題２の証明
最後に補題２を証明します．２通りの方法で証明してみましょう．
座標平面を用いた証明
証明．
以下の図のように，円の中心を$(0,0)$, $P$ の座標を $(s,t)$ とし，$l_1$ が $y$ 軸に直交，$h_1$ が $x$ 軸に直交するように座標を設定する．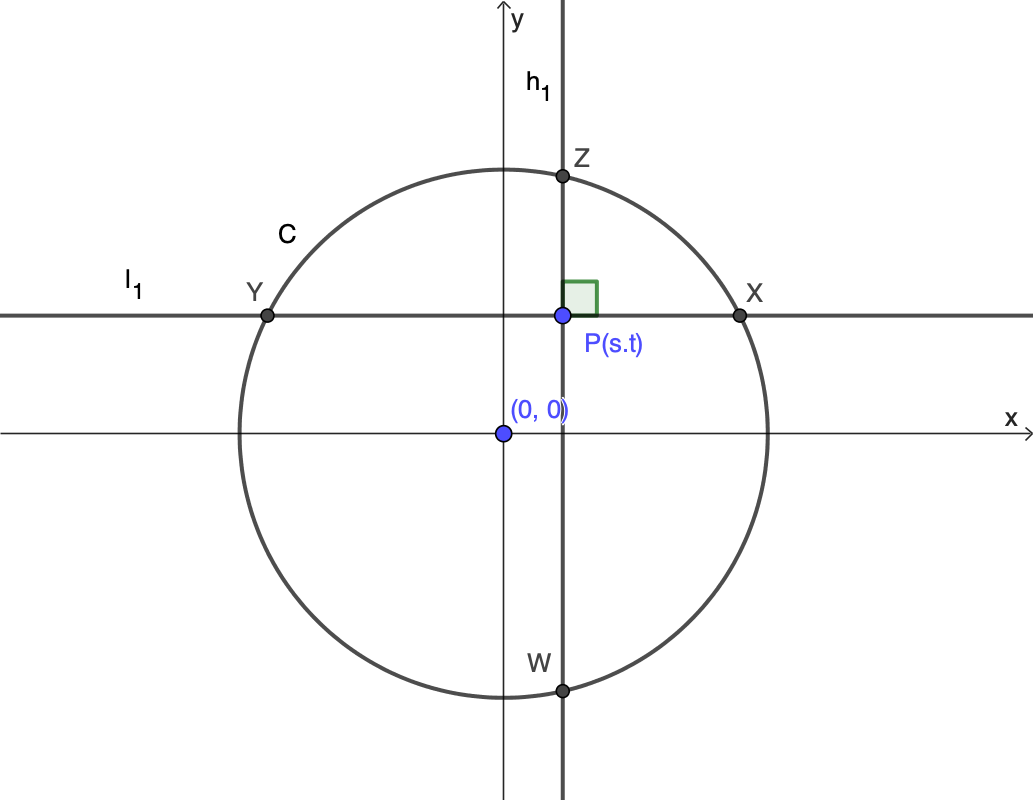
回転または裏返しを考えることにより，$$\begin{aligned}&0 \leq s \leq 1,\\&0 \leq t \leq 1,\\ &0 \leq s^2 + t^2 \leq 1 \end{aligned}$$ が成り立つと仮定しても一般性を失わないのでそうする．点 $X,\ Y,\ Z,\ W$ を図のように定める．このとき，$$\begin{aligned} &PX = \sqrt{1-t^2}-s \\ &PY = \sqrt{1-t^2}+s \\&PZ = \sqrt{1-s^2}-t \\ &PW = \sqrt{1-s^2}+t\end{aligned}$$だから，それぞれ $2$ 乗して辺々足すことにより$$PX^2+PY^2+PZ^2+PW^2=4$$を得る．
初等幾何的な証明
証明．
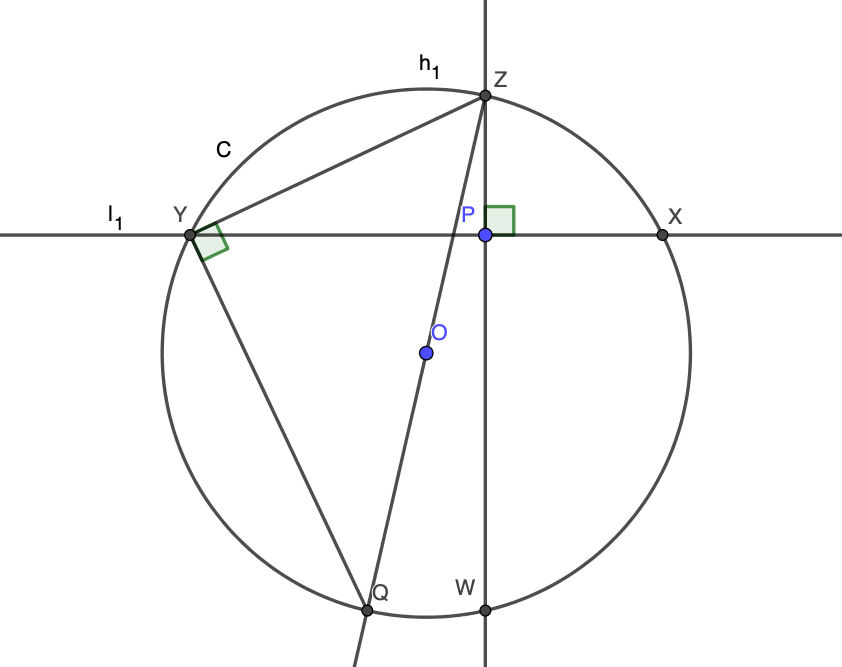円 $C$ の中心を $O$ とし, 直線 $ZO$ と円 $C$ の共有点のうち $Z$ と異なるものを $Q$ とする．まず，$XW = YQ$ であることを示そう．
$XW = YQ$ の証明
$\angle XYW =\angle YXQ$ をいえば十分．
円周角の定理より，$\angle XYW = \angle XZW$, $\angle YXQ = \angle YZQ$ である．よってあとは $\angle XZW =\angle YZQ$ をいえばよい．いま $\angle ZYQ = \angle ZPX = \pi/2$ であり，また円周角の定理から $\angle ZQY = \angle ZXY$ である．したがって三角形 $ZQY$ と三角形 $ZXP$ は相似であることが分かる．よって $\angle XYW =\angle YXQ$ である．
$PX^2+PY^2+PZ^2+PW^2=4$ の証明
三角形 $ZYP$，三角形 $XPW$ は直角三角形だから，三平方の定理を用いて$$PX^2+PY^2+PZ^2+PW^2 =YZ^2 + XW^2 $$である．$XW = YQ$ だったから右辺は $YZ^2+YQ^2$ に等しい．さらに三角形 $ZYQ$ は直角三角形だから三平方の定理より $YZ^2+YQ^2=ZQ^2=4$ である．以上より$$PX^2+PY^2+PZ^2+PW^2 =4 $$ が分かった．
