最近は曲線刃を採用したハサミを見かけることが多くなりました．$2$ 枚の刃のなす角がハサミの開き具合に依らず一定になっており，このことがハサミの切れ味の良さにつながっているのだそうです．このようなハサミの刃を表す曲線は，数式を用いるとどのように書けるのでしょうか．本記事ではこの問いについて考えます．
導出
曲線が満たす微分方程式
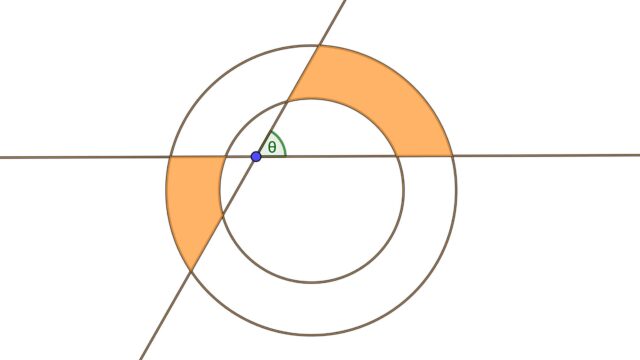
ハサミの刃を表す曲線を $c(t)=(x(t),y(t))$ とする．$c(t)$ が満たすべき条件は各 $t$ で 位置ベクトル $c(t)$ と 速度ベクトル $\frac{dc}{dt}(t)$ のなす角が一定であることである．この角度を $0<\alpha<\frac{\pi}{2}$ とおこう（図1）．
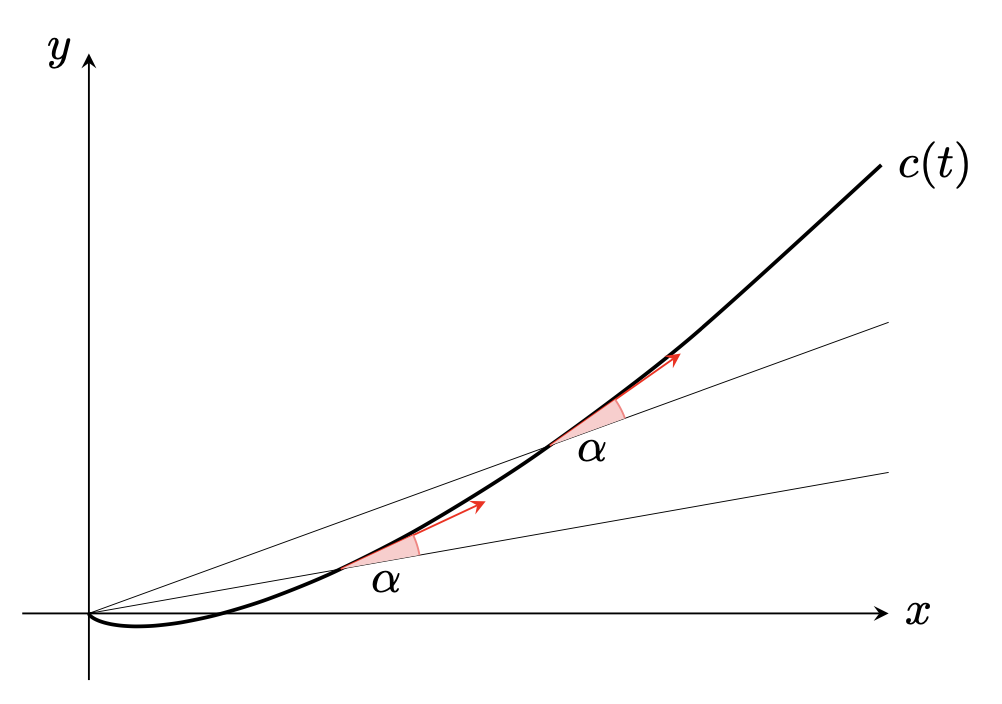図1. 曲線 $c(t)$ のグラフ．このグラフは $\alpha=15^\circ$ としたものであり，実際のハサミの刃の形に非常に近い．微分方程式を書くと次のようになる：$$\left\{\begin{eqnarray}\frac{dx}{dt}=x \cos {\alpha}-y \sin{\alpha} \\\frac{dy}{dt}=x \sin {\alpha}+y \cos{\alpha}\end{eqnarray}\right. \tag{1}\label{eq1}$$
これを解けば良いわけだが，$z(t)=x(t)+iy(t)$ ($i$ は虚数単位)とおいて複素関数の微分方程式とみると見通し良く解くことができる．実際，\eqref{eq1} は$$\frac{dz}{dt} = (\cos{\alpha}+i\sin{\alpha}) z \tag{2}\label{eq2}$$と書ける．これは変数分離型の微分方程式であり，一般解は次のように表される：$$z(t)=C \exp{((\cos{\alpha}+i\sin{\alpha})t)} \ (C \in \mathbb{C}).$$
極方程式で表す
ここで特に$C=1$としたときの解$$z(t)=\exp{((\cos{\alpha}+i\sin{\alpha})t)}\tag{3}\label{eq3}$$について考えよう．これはどのような曲線を表すのだろうか．$$|z(t)|=\exp{((\cos{\alpha})t)},\ \arg{z(t)}=(\sin{\alpha})t$$であることより\eqref{eq3}で表される曲線は，極方程式で書くと$$r=\exp{\left(\frac{\theta}{\tan{\alpha}}\right)}$$となることが分かる．これはベルヌーイの対数螺旋と呼ばれる曲線である．
おわりに
以上の考察と，コーシーリプシッツの定理より\eqref{eq2}の解が一意的であることを合わせて，対数螺旋が条件を満たす唯一の曲線であることが分かった．
