バウムクーヘンの定理

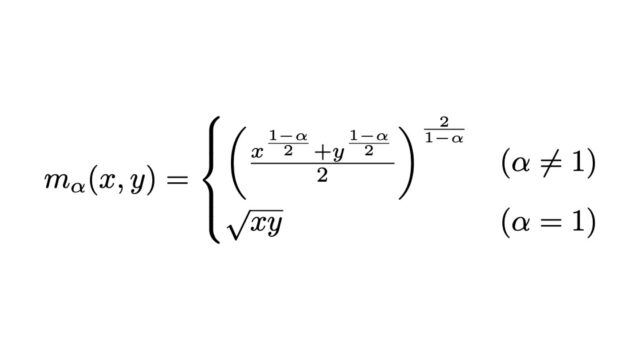
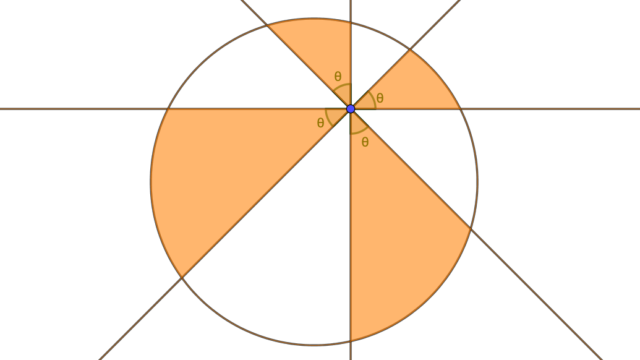
以前紹介したピザの定理の円環領域バージョンとして，バウムクーヘンの定理（Baumukuchen Theorem）が知られています．本記事ではバウムクーヘンの定理の主張と証明をご紹介します．

バウムクーヘンの定理

バウムクーヘンの定理の主張は以下のとおりです．

定理１（バウムクーヘンの定理）

$0<r<R$ とし，以下の図のように平面上の点 $O$ を中心とする半径 $r$ の円を $C$, 半径 $R$ の円を $D$ とする．また，点$P$ を $C$ 上または $C$ の内側にある点とする．$l,\ m$ を $P$ を通る直線とし，$l,\ m$ のなす（小さいほうの）角を $\theta$ とする．このとき，橙色の領域の面積は $(R^2-r^2)\theta$ である．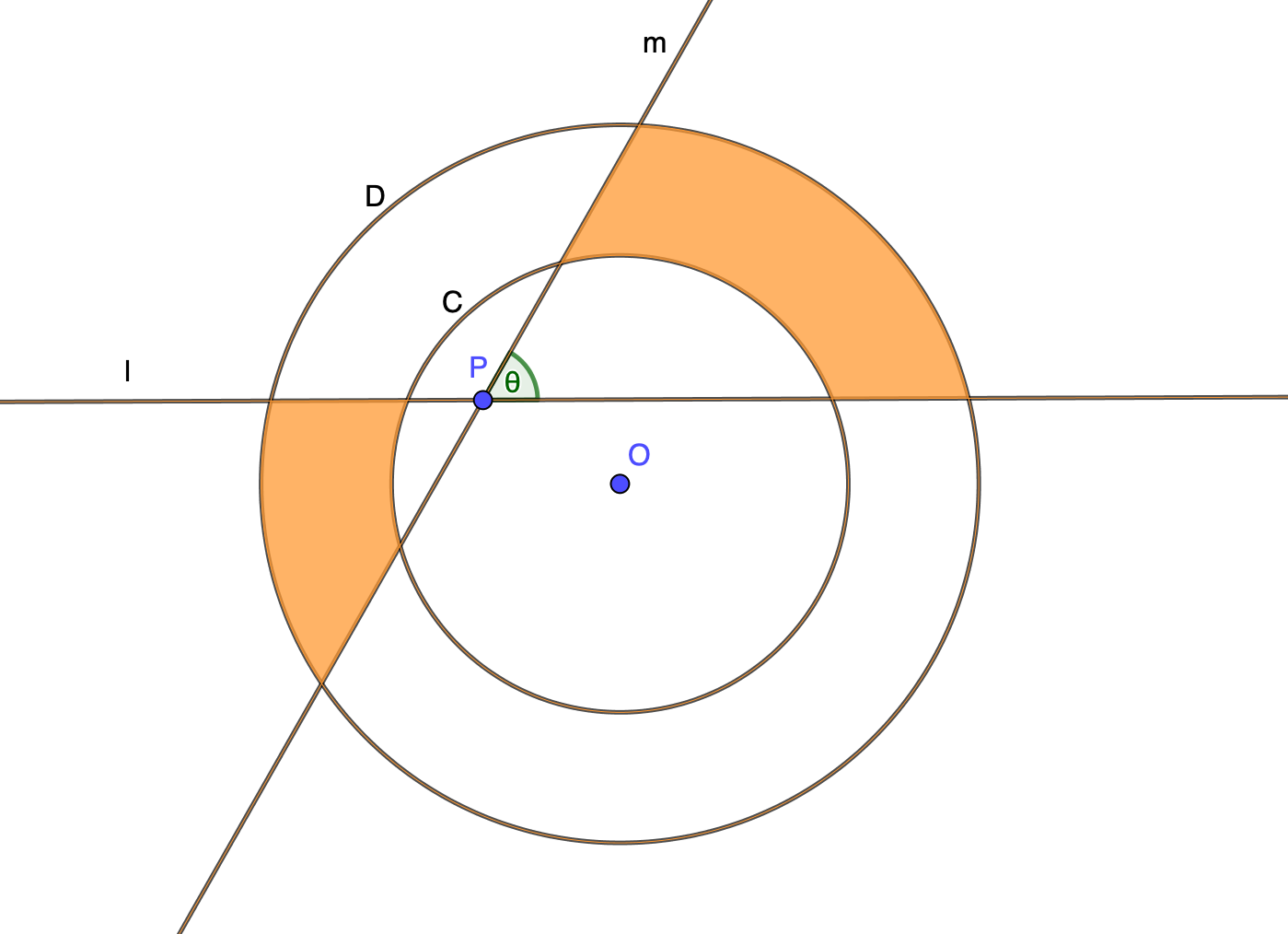

バームクーヘンの定理の証明

証明には次の補題を用います．

補題２

点 $O,P$，円 $C,D$ および直線 $l$ を定理1と同様に定める．また，$C$ と $l$ の共有点を $X,Y$ とし，$D$ と $l$ の共有点を $Z,W$ とする（$X,Z$ が $P$ に対して $l$ 上おなじ側にくるように名付ける）．このとき$$PZ^2+PW^2-PX^2-PY^2=2(R^2-r^2)$$が成り立つ．

補題２の証明．

以下の図のように$O$の座標を$(0,0)$,$P$の座標を$(s,t)$ （$s^2+t^2 \leq r^2$）とし，$l$と $x$ 軸が平行になるように座標を設定する．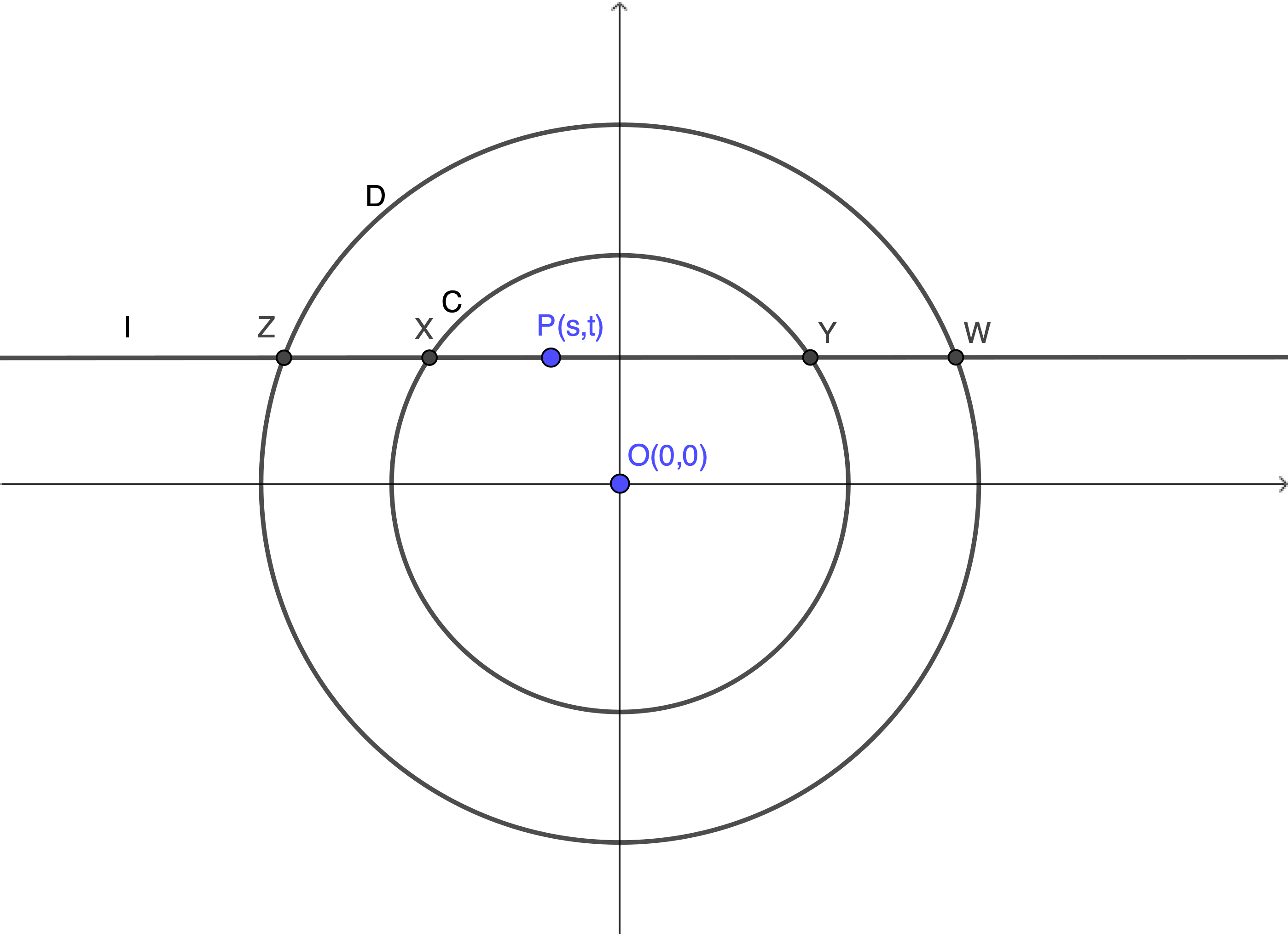

このとき，$$\begin{aligned}PX^2 &=(s+\sqrt{r^2-t^2})^2\\ PY^2 &=(s-\sqrt{r^2-t^2})^2\\ PZ^2 &=(s+\sqrt{R^2-t^2})^2\\ PW^2&=(s-\sqrt{R^2-t^2})^2\end{aligned}$$であるから，$$PZ^2+PW^2-PX^2-PY^2=2(R^2-r^2)$$を得る．

補題２を用いて定理１を証明しましょう．

定理１の証明．

点 $X(\theta),Y(\theta),Z(\theta),W(\theta)$ を以下の図のように定める．

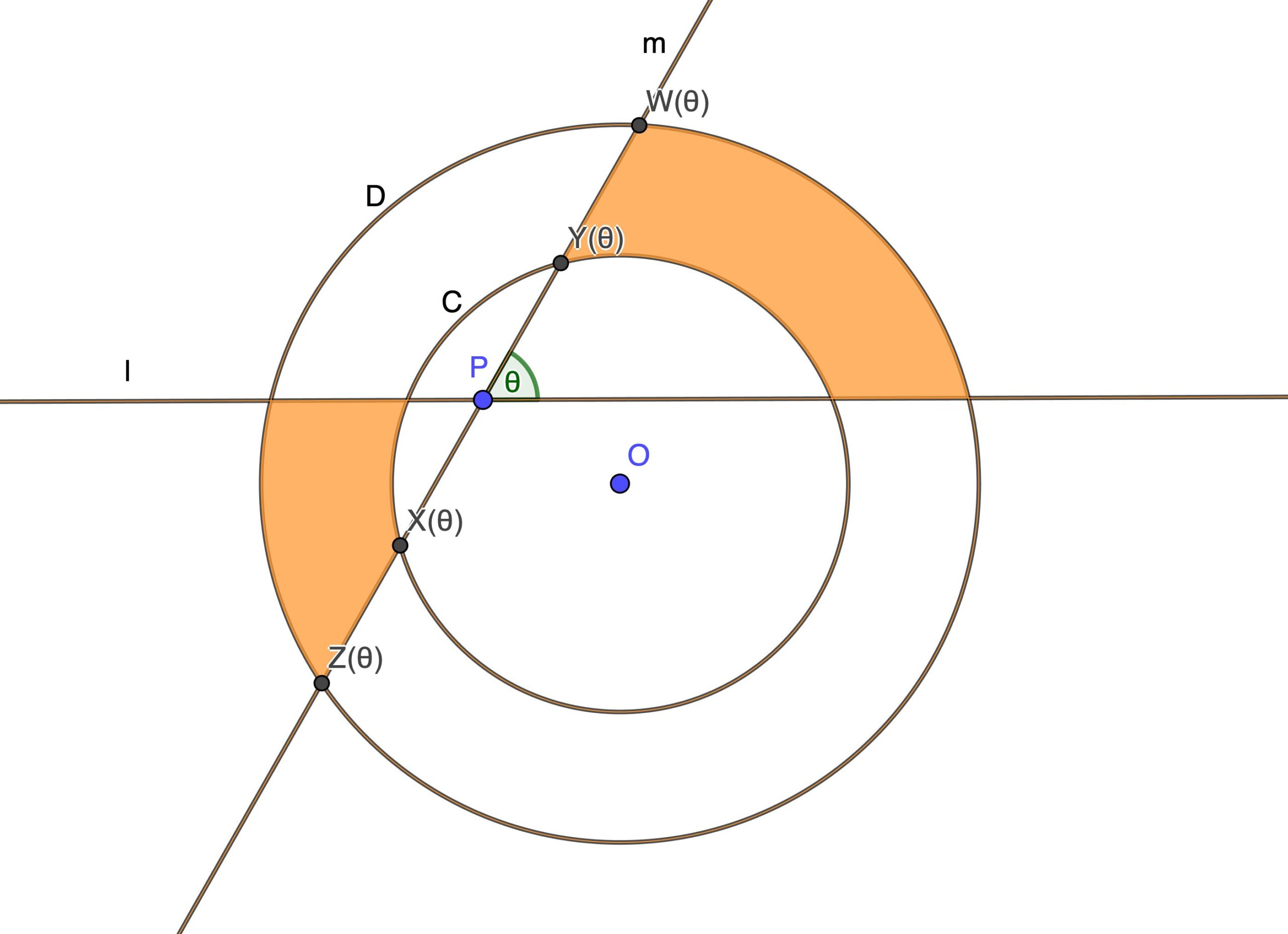極方程式の面積公式から橙色の領域の面積（以下$S(\theta)$とおく）は$$\begin{aligned}\frac{1}{2} \int_0^\theta \{ PZ(\theta)^2+PW(\theta)^2\\ \quad -PX(\theta)^2-PY(\theta)^2\}dt\end{aligned}$$である．ここで補題２より右辺の非積分関数の値は $\theta$ に依存せず $2(R^2-r^2)$ なので，$$\begin{aligned}S(\theta)&= \frac{1}{2}\int_0^\theta 2(R^2-r^2)dt \\&=(R^2-r^2)\theta\end{aligned}$$である．定理１が示せた．