本記事ではシムソンの定理の主張とその証明を紹介します.
シムソンの定理
シムソンの定理の主張は次のとおりです.
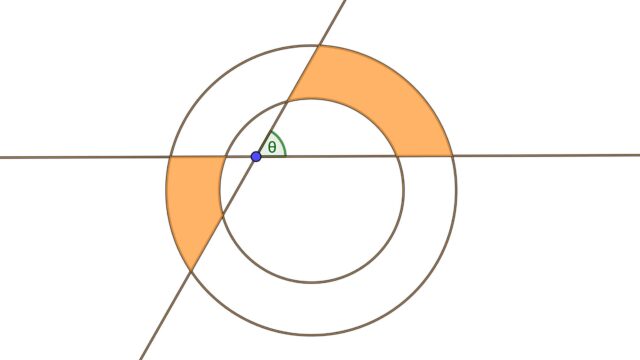
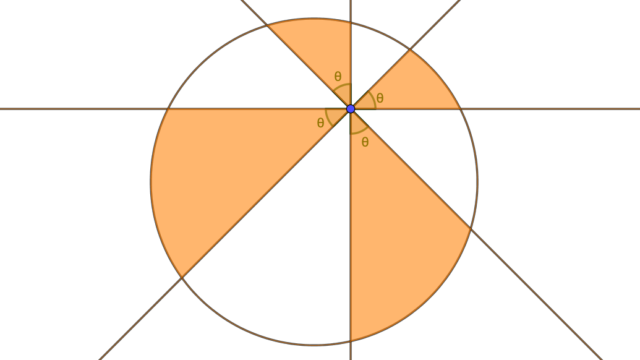
平面上の三角形 $ABC$ および 点 $P$ に対し,$P$ から直線 $AB,BC,CA$ に下ろした垂線の足をそれぞれ $X,Y,Z$ とする.このとき以下は同値.
- 点 $P$ は三角形 $ABC$ の外接円上にある.
- $X,Y,Z$ は共線である.

ちなみに $X,Y,Z$ を通る直線はシムソン線と呼ばれています.
シムソンの定理の証明
初等幾何による証明
さっそく定理を証明しましょう.初等幾何的な方法で示します.
証明.
円周角の定理より $(1) \Leftrightarrow \angle APC=\angle ABC$ である.いま $\angle PXB=\angle PYB=90^\circ$ だから $X,P,B,Y$ は共円である.したがって $\angle XPY=\angle XBY=\angle ABC$ が分かるので $(1)$ は $\angle APC= \angle XPY$ と同値であり,さらにこれは $\angle APX= \angle CPY \cdots (\bigstar)$ と同値である.また,$\angle AZP=\angle AXP=90^\circ$ より $A,Z,P,X$ が共円であることが分かるので,$\angle APX=\angle AZX$ である.同様に $C,Z,P,Y$ が共円であることから $\angle CPY=\angle CZY$ を得る.これらより $(\bigstar)\Leftrightarrow \angle AZX=\angle CZY $ が分かるが,右辺はさらに $(2)$ と同値である.
複素数平面を用いた証明
複素数平面を用いた$(1)\Rightarrow(2)$の証明で,あまり知られていない(と思われる)が上手なやり方があるのでご紹介します.
証明.
シムソンの定理の $(1)\Rightarrow(2)$ を示す.複素数平面上の中心$\frac{1}{2}$,半径$\frac{1}{2}$の円を考える.点 $A,B,C$ はその円周上にあるものとし,点 $P$ は $0$ に対応するとして一般性を失わないからそうする.点 $A,B,C$ に対応する複素数をそれぞれ $\alpha,\beta,\gamma$ とおく.このとき $X,Y,Z$ に対応する複素数はそれぞれ $\alpha\beta,\beta\gamma,\gamma\alpha$ となることに注意する.いま $0,\alpha,\beta,\gamma$ が共円であることから$$\beta(\alpha-\gamma)\overline{\alpha}\overline{(\beta-\gamma)}=\overline{\beta}\overline{(\alpha-\gamma)}\alpha(\beta-\gamma)$$すなわち$$(\alpha\beta-\beta\gamma)(\overline{\alpha\beta-\gamma\alpha})=(\alpha\beta-\gamma\alpha)(\overline{\alpha\beta-\beta\gamma})$$が分かる.ところがこれは $X,Y,Z$ が共線であることに他ならない.