円に内接する三角形のうち，面積が最大となるのは正三角形であるということが知られています．本記事ではこのことを証明します．
証明
半径 $1$ の円を考え，その中心を $O$ とする．また，$P_1,P_2,P_3$ をその円周上の点とする．図１のように角 $P_1OP_2,P_2OP_3,P_3OP_1$ をそれぞれ $\theta_1,\theta_2,\theta_3$ とする．
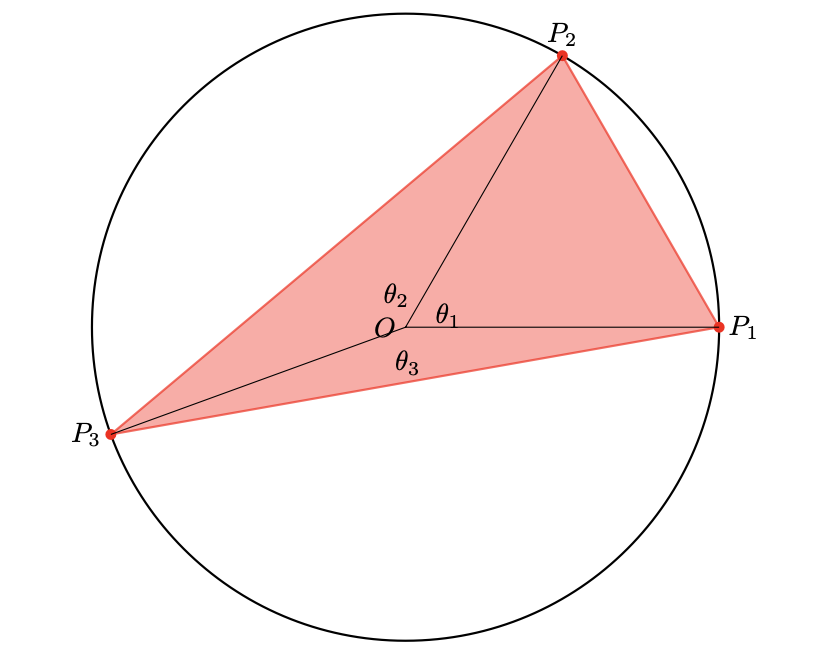図1このとき $P_1,P_2,P_3$ がなす三角形の面積 $S(\theta_1,\theta_2,\theta_3)$ は$$S(\theta_1,\theta_2,\theta_3)=\frac{1}{2}\left(\sin{\theta_1}+\sin{\theta_2}+\sin{\theta_3}\right)$$で表される．
- $\theta_i \geq 0\quad (i=1,2,3)$
- $\theta_1+\theta_2+\theta_3=2\pi$
の下で $S(\theta_1,\theta_2,\theta_3)$ を最大化する $\theta_1,\theta_2,\theta_3$ を求めればよい．
証明１（イェンセンの不等式を利用）
簡単な考察によりある $i \in \{1,2,3\}$ で $\theta_i>\pi$ ならば $S(\theta_1,\theta_2,\theta_3)$ は最大とならないことが分かるので，既に上で述べた条件に加えて $\forall i \in \{1,2,3\},\ \theta_i \leq \pi$ を仮定してよい．$$\sin:[0,\pi] \to \mathbb{R},\ t \mapsto \sin{t}$$の凸性からイェンセンの不等式が使えて，$$\begin{align}&S(\theta_1,\theta_2,\theta_3)\\&=\frac{1}{2}\left(\sin{\theta_1}+\sin{\theta_2}+\sin{\theta_3}\right)\\&\leq \frac{1}{2} \left(3\sin{\frac{\theta_1+\theta_2+\theta_3}{3}}\right)\\&=\frac{3}{2} \sin\frac{2\pi}{3}\\&=\frac{3\sqrt{3}}{4}\end{align}$$となる．等号成立の必要十分条件は $\theta_1=\theta_2=\theta_3=\frac{2\pi}{3}$ であり，円に内接する面積最大の三角形は正三角形であることが分かった．
証明２
$\theta_1,\theta_2,\theta_3$ が動く領域のコンパクト性と $S(\theta_1,\theta_2,\theta_3)$ の連続性から $S(\theta_1,\theta_2,\theta_3)$ を最大化する $\theta_1,\theta_2,\theta_3$ の存在が従う．あとは正三角形以外の三角形では面積が最大とならないことを示せばよい．対称性から $\theta_1 \neq \theta_2$ と仮定し $S(\theta_1,\theta_2,\theta_3)$ が最大値でないことを確かめれば十分である．いま $\theta:=(\theta_1+\theta_2)/2$ とすると$$S(\theta_1,\theta_2,\theta_3) < S(\theta,\theta,\theta_3)$$だから $S(\theta_1,\theta_2,\theta_3)$ が最大値でないことがわかる（図２参照）．
図２．右の三角形の方が$P_1P_3$ を底辺としたときの高さが大きいため，面積も大きい．
一般化
より一般に，次のことが知られています．
$n$ を自然数とする．円に内接する $n$ 角形のうち面積が最大のものは正 $n$ 角形である．
証明は三角形の場合と同様にして可能です．
また最近はこの事実を日本の高校生たちが（ほとんど）高校までの知識のみで示したことで話題になりました．彼らの論文は以下のURLから参照できますので，興味のある方はぜひ読んでみてください！
